Bitcoin

Bitcoin
Bitcoin

Bubble Sort

Sorting is ordering a list of objects. We can distinguish two types of sorting. If the number of objects is small enough to fits into the main memory, sorting is called internal sorting. If the number of objects is so large that some of them reside on external storage during the sort, it is called external sorting. In this chapter we consider the following internal sorting algorithms
  • Bucket sort
  • Bubble sort
  • Insertion sort
  • Selection sort
  • Heapsort
  • Mergesort

O(n) algorithms

Bucket Sort

Suppose we need to sort an array of positive integers {3,11,2,9,1,5}. A bucket sort works as follows: create an array of size 11. Then, go through the input array and place integer 3 into a second array at index 3, integer 11 at index 11 and so on. We will end up with a sorted list in the second array.
Suppose we are sorting a large number of local phone numbers, for example, all residential phone numbers in the 412 area code region (about 1 million) We sort the numbers without use of comparisons in the following way. Create an a bit array of size 107. It takes about 1Mb. Set all bits to 0. For each phone number turn-on the bit indexed by that phone number. Finally, walk through the array and for each bit 1 record its index, which is a phone number.
We immediately see two drawbacks to this sorting algorithm. Firstly, we must know how to handle duplicates. Secondly, we must know the maximum value in the unsorted array.. Thirdly, we must have enough memory - it may be impossible to declare an array large enough on some systems.
The first problem is solved by using linked lists, attached to each array index. All duplicates for that bucket will be stored in the list. Another possible solution is to have a counter. As an example let us sort 3, 2, 4, 2, 3, 5. We start with an array of 5 counters set to zero.
  0    1    2    3    4    5  
 0 0 0 0 0 0
Moving through the array we increment counters:
  0    1    2    3    4    5  
 0 0 2 2 1 1
Next,we simply read off the number of each occurrence: 2 2 3 3 4 5.

O(n2) algorithms

Bubble Sort

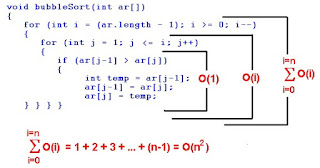
The algorithm works by comparing each item in the list with the item next to it, and swapping them if required. In other words, the largest element has bubbled to the top of the array. The algorithm repeats this process until it makes a pass all the way through the list without swapping any items.

void bubbleSort(int ar[])
{
   for (int i = (ar.length - 1); i >= 0; i--)
   {
      for (int j = 1; j ≤ i; j++)
      {
         if (ar[j-1] > ar[j])
         {
              int temp = ar[j-1];
              ar[j-1] = ar[j];
              ar[j] = temp;
   } } } }
Example. Here is one step of the algorithm. The largest element - 7 - is bubbled to the top:
7, 5, 2, 4, 3, 9
5, 7, 2, 4, 3, 9
5, 2, 7, 4, 3, 9
5, 2, 4, 7, 3, 9
5, 2, 4, 3, 7, 9
5, 2, 4, 3, 7, 9
The worst-case runtime complexity is O(n2). See explanation below 
Java program to bubble sort: This code sorts numbers inputted by user using Bubble sort algorithm.

Java programming code

import java.util.Scanner;
 
class BubbleSort {
  public static void main(String []args) {
    int n, c, d, swap;
    Scanner in = new Scanner(System.in);
 
    System.out.println("Input number of integers to sort");
    n = in.nextInt();
 
    int array[] = new int[n];
 
    System.out.println("Enter " + n + " integers");
 
    for (c = 0; c < n; c++) 
      array[c] = in.nextInt();
 
    for (c = 0; c < ( n - 1 ); c++) {
      for (d = 0; d < n - c - 1; d++) {
        if (array[d] > array[d+1]) /* For descending order use < */
        {
          swap       = array[d];
          array[d]   = array[d+1];
          array[d+1] = swap;
        }
      }
    }
 
    System.out.println("Sorted list of numbers");
 
    for (c = 0; c < n; c++) 
      System.out.println(array[c]);
  }
}
Complexity of bubble sort is O(n2) which makes it a less frequent option for arranging in sorted order when quantity of numbers is high.
import java.util.Arrays;
 
class Sort
{
  public static void main(String args[])
  {
    int data[] = { 4, -5, 2, 6, 1 };
 
    Arrays.sort(data);
 
    for (int c: data) 
    {
      System.out.println(c);
    }
  }
}

ANOTHER PROGRAM ON BUBBLE SORT
In bubble sort algorithm, array is traversed from first element to last element. Here, current element is compared with the next element. If current element is greater than the next element, it is swapped.
  1. public class BubbleSortExample {  
  2.     static void bubbleSort(int[] arr) {  
  3.         int n = arr.length;  
  4.         int temp = 0;  
  5.          for(int i=0; i < n; i++){  
  6.                  for(int j=1; j < (n-i); j++){  
  7.                           if(arr[j-1] > arr[j]){  
  8.                                  //swap elements  
  9.                                  temp = arr[j-1];  
  10.                                  arr[j-1] = arr[j];  
  11.                                  arr[j] = temp;  
  12.                          }  
  13.                           
  14.                  }  
  15.          }  
  16.   
  17.     }  
  18.     public static void main(String[] args) {  
  19.                 int arr[] ={3,60,35,2,45,320,5};  
  20.                  
  21.                 System.out.println("Array Before Bubble Sort");  
  22.                 for(int i=0; i < arr.length; i++){  
  23.                         System.out.print(arr[i] + " ");  
  24.                 }  
  25.                 System.out.println();  
  26.                   
  27.                 bubbleSort(arr);//sorting array elements using bubble sort  
  28.                  
  29.                 System.out.println("Array After Bubble Sort");  
  30.                 for(int i=0; i < arr.length; i++){  
  31.                         System.out.print(arr[i] + " ");  
  32.                 }  
  33.    
  34.         }  
  35. }  
Output:
Array Before Bubble Sort
3 60 35 2 45 320 5 
Array After Bubble Sort
2 3 5 35 45 60 320

ANOTHER CODE FOR BUBBLE SORT
public class MyBubbleSort {
    // logic to sort the elements
    public static void bubble_srt(int array[]) {
        int n = array.length;
        int k;
        for (int m = n; m >= 0; m--) {
            for (int i = 0; i < n - 1; i++) {
                k = i + 1;
                if (array[i] > array[k]) {
                    swapNumbers(i, k, array);
                }
            }
            printNumbers(array);
        }
    }
    private static void swapNumbers(int i, int j, int[] array) {
        int temp;
        temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
    private static void printNumbers(int[] input) {
         
        for (int i = 0; i < input.length; i++) {
            System.out.print(input[i] + ", ");
        }
        System.out.println("\n");
    }
    public static void main(String[] args) {
        int[] input = { 4, 2, 9, 6, 23, 12, 34, 0, 1 };
        bubble_srt(input);
    }
}

Output:
2, 4, 6, 9, 12, 23, 0, 1, 34, 

2, 4, 6, 9, 12, 0, 1, 23, 34, 

2, 4, 6, 9, 0, 1, 12, 23, 34, 

2, 4, 6, 0, 1, 9, 12, 23, 34, 

2, 4, 0, 1, 6, 9, 12, 23, 34, 

2, 0, 1, 4, 6, 9, 12, 23, 34, 

0, 1, 2, 4, 6, 9, 12, 23, 34, 

0, 1, 2, 4, 6, 9, 12, 23, 34, 

0, 1, 2, 4, 6, 9, 12, 23, 34, 

0, 1, 2, 4, 6, 9, 12, 23, 34,

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)

Facebook